Поиск пути — не самая тривиальная задача. В данной статье я постараюсь описать основные принципы решения данной задачи на основе рассмотрения нескольких хороших, надежных алгоритмов, которые заслужили большую известность.

Алгоритмы поиска маршрута движения

Начинать изучение алгоритмов поиска пути лучше не с самых эффективных, а с простейших: их изучение позволяет постепенно вводить нужные концепции и разобраться, как решаются различные проблемы.

Типичная проблема в поиске пути — обход препятствий. Самое простое — игнорировать препятствия до столкновения с ними. Все, что необходимо знать в каждый момент, — это относительные положения объекта и его цели, признак того, что мы уперлись в препятствие, а также стратегию обхода препятствия при встрече с ним. Для многих игровых ситуаций этого достаточно.

Различные стратегии обхода препятствий включают в себя:

Перемещение в случайном направлении; Трассировку вокруг препятствия; Надежную трассировку.

Трассировка — это процесс следования из точки A в точку B и нахождения надежного и по возможности наилучшего пути между точками.

Хотя техник обхода препятствий, перечисленных выше, часто достаточно, существуют ситуации, в которых единственно разумный подход — планирование всего пути перед началом перемещений. Кроме того, эти методы не могут решить проблему взвешенных областей, которая состоит не столько в обходе препятствий, сколько в поиске пути с наименьшей стоимостью среди других вариантов, где стоимость местности может изменяться.

К счастью, в областях теории графов и обычного ИИ имеется несколько алгоритмов, которые могут решить проблему и сложных препятствий, и взвешенных областей. В литературе многие из этих алгоритмов представлены в терминах изменения состояний или прохода по узлам графа. Применение этих алгоритмов к поиску пути в геометрическом пространстве требует простой адаптации: состояние или узел графа представляют объект, находящийся в определенной клетке, и передвижение в соседние клетки соответствует перемещению в соседние состояния или смежные узлы.

Рассмотрим эти алгоритмы.

Поиск в ширину

Начиная со стартового узла этот алгоритм сначала перебирает все непосредственно соседние узлы, затем все узлы в двух шагах, затем в трех, и так далее, пока цель не достигнута. При реализации для каждого узла его непроверенные соседи помещаются в список Open, который чаще всего представляет собой FIFO-очередь.

Карта.

Очередь — структура данных с дисциплиной доступа к элементам «первый пришел — первый вышел» (FIFO, First In — First Out). Добавление элемента (принято обозначать словом enqueue) возможно лишь в конец очереди, выборка — только из начала очереди (что принято называть dequeue, при этом выбранный элемент из очереди удаляется). В языке программирования очередь может быть реализована как массив или односвязный список записей.

Поиск в ширину.

Если рассматривать карту поиска, можно заметить, что он находит путь вокруг препятствий, и этот путь — кратчайший или один из нескольких кратчайших в длину путей, если все шаги имеют одинаковую стоимость. Но есть и недостатки. Первый из них состоит в том, что поиск идет равномерно во всех направлениях, вместо того чтобы стремиться в сторону цели. Другая проблема в том, что не все шаги равны, по крайней мере, шаги по диагонали должны быть длиннее ортогональных. Это приводит к появлению таких артефактов в результате работе алгоритма, как резкие неестественные повороты при движении. При использовании классического варианта поиска в ширину избавиться от них практически невозможно. Но, скажем, на гексагональном поле, на котором все соседи узла равноправны, этот алгоритм достаточно хорош.

Алгоритм Дийкстры

Е. Дийкстра разработал классический алгоритм для прохода по графам, ребра которых имеют различный вес.

Е. Дийкстра — профессор Edsger Wybe Dijkstra, выдающийся пионер компьютерной науки и промышленности.

Карта. Различными цветами показаны области с разными стоимостями движения по ним.

На каждом шаге он ищет необработанные узлы, близкие к стартовому, затем просматривает соседей найденного узла и устанавливает или обновляет их соответствующие расстояния от старта. Этот алгоритм имеет два преимущества по сравнению с поиском в ширину: он принимает во внимание стоимость или длину пути и обновляет узлы, если к ним найден лучший путь. Для реализации вместо списка Open с очередью FIFO используют приоритетную очередь, где извлеченный узел имеет наилучшее значение — для алгоритма Дийкстры это наименьшая стоимость пути от старта.

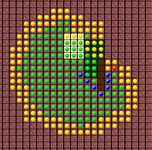Поиск пути по Дийкстре

Приоритетная очередь (или очередь с приоритетами) — в реальных задачах иногда возникает необходимость в формировании очередей, отличных от FIFO или LIFO. Порядок выборки элементов из таких очередей определяется приоритетами элементов. Приоритет в общем случае может быть представлен числовым значением, которое вычисляется либо на основании значений каких-либо полей элемента, либо на основании внешних факторов. Так, и FIFO, и LIFO-очереди могут трактоваться как приоритетные очереди, в которых приоритет элемента зависит от времени его включения в очередь. При выборке элемента всякий раз выбирается элемент с наибольшим приоритетом.

Однако, как и поиск в ширину, этот алгоритм игнорирует направление к цели.

Алгоритм Дийкстры уже более гибок в использовании. Так, изменяя вес ячеек карты и функцию их сравнения, можно довольно эффективно бороться с нежелательными явлениями в работе алгоритма. В частности, можно придать маршруту движения более естественный, плавный характер, увеличивая или уменьшая цену пути за преимущественное движение по диагоналям, а не по прямым, когда того требует «здравый смысл».

Алгоритм «лучший-первый»

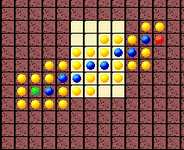Может, первый иногда и лучший, но не всегда и не во всем.

Это — первый рассматриваемый эвристический поиск, который принимает во внимание знания о пространстве поиска для направления своих усилий.

Еще одна странная особенность.

Эвристические алгоритмы — приемы решения проблемных (творческих, нестандартных, креативных) задач в условиях неопределенности, которые обычно противопоставляются формальным методам решения, опирающимся, например, на точные математические алгоритмы. Эвристические методы увеличивают вероятность получения работоспособного — но не всегда оптимального — решения творческой задачи, возникшей, например, из-за неразработанности конкретной теории, неполноты или недостоверности исходных данных.

Он похож на алгоритм Дийкстры, за исключением того, что узлы в списке Open оцениваются по приблизительному оставшемуся расстоянию до цели. Эта оценка также не требует наличия обновлений, в отличие от алгоритма Дийкстры. Это самый быстрый из всех планирующих алгоритмов, рассмотренных ранее, который направляется по прямой к цели. Но у него есть и свои слабости. Он не принимает во внимание накопленную стоимость пути, направляясь по прямой через зону с высокой стоимостью, а не обходя ее. Можно увидеть, что в некоторых случаях найденный путь вокруг препятствия не прямой, а изгибается вокруг препятствия.

В общем — простой, но «туповатый» алгоритм. Подойдет для простых карт.

Алгоритм А*

Очень хорошие результаты дает алгоритм для поиска оптимальных путей в различных пространствах, называемый A* (читается как «А-звездочка»). Этот эвристический поиск сортирует все узлы по приближению наилучшего маршрута, идущего через этот узел. Типичная формула эвристики выражается в виде:

f(n) = g(n) + h(n)

где:

f(n) — значение оценки, назначенное узлу n;

g(n) — наименьшая стоимость прибытия в узел n из точки старта;

h(n) — эвристическое приближение стоимости пути к цели от узла n.

Таким образом, этот алгоритм сочетает в себе учет длины предыдущего пути из алгоритма Дийкстры с эвристикой из алгоритма «лучший-первый». Так как некоторые узлы могут обрабатываться повторно (для поиска оптимальных путей к ним позднее), необходимо ввести новый список Closed для их отслеживания.

A* имеет множество интересных свойств. Он гарантированно находит кратчайший путь до тех пор, пока оценка h(n) надежна, то есть он никогда не превышает действительного оставшегося расстояния до цели. Этот алгоритм наилучшим образом использует эвристику: ни один другой алгоритм не раскроет меньшее число узлов, не учитывая узлов с одинаковой стоимостью. На примерах можно увидеть, как A* справляется с ситуациями, проблемными для других алгоритмов.

Довольно интересный случай.

На практике A* оказывается очень гибким. Рассмотрим различные части алгоритма. Состоянием может быть ячейка или позиция, которую занимает объект. Но при необходимости состоянием с таким же успехом может быть ориентация и скорость (например, при поиске пути для танка или любой другой машины — их радиус поворота становится хуже при большей скорости).

Соседние состояния могут изменяться в зависимости от игры и локальной ситуации. Смежные позиции могут быть исключены, потому что они непроходимы. Некоторые типы местности могут быть непроходимыми для некоторых объектов, но проходимыми для других; объекты, которые медленно разворачиваются, не могут перемещаться во все соседние клетки.

Стоимость перехода из одной позиции в другую может представлять что угодно: обычное расстояние между позициями; стоимость по времени или топливу на перемещение; штрафы за проезд через нежелательную область (например, точки в пределах вражеской артиллерии); бонусы за проезд через предпочтительные области (например, исследование новой области или захват контроля над неконтролируемыми зонами); наконец, эстетические соображения (например, если диагональные перемещения такие же по стоимости, как и ортогональные, все равно лучше сделать их стоимость больше, для того чтобы пути выглядели более прямыми и естественными).

Поиск произведен — маршрут проложен.

В качестве оценки обычно берется минимальное расстояние между текущим узлом и целью, умноженному на минимальную стоимость передвижения между узлами. Это гарантирует допустимость эвристики h(n). (На карте с квадратными клетками, где объекты могут занимать только точки на сетке, минимальным расстоянием будет не геометрическое расстояние, а минимальное число ортогональных и диагональных перемещений между двумя точками.)

Цель не обязательно должна быть единственной позицией, но может состоять из множества позиций. Тогда приближение должно равняться минимуму приближений ко всем возможным целям. Легко реализовать ограничение по стоимости пути или по расстоянию, или по обоим признакам. Из моего непосредственного опыта я знаю, что А* хорошо работает для большого числа типов путей в военных играх (wargames) и стратегиях.

Существуют ситуации, в которых A* не может работать хорошо по различным причинам. Требования работы в реальном масштабе времени для некоторых игр, а также ограничения по памяти и процессорному времени в некоторых из них создают проблемы для хорошей работы даже А*. Большая карта может требовать тысячи ячеек в списках Open и Closed, для чего может оказаться недостаточно места. Даже если для них окажется достаточно памяти, алгоритмы для работы с этими списками могут оказаться неэффективными.

Качество работы алгоритма сильно зависит от качества эвристического приближения h(n). Если h близко к истинной стоимости оставшегося пути, то эффективность будет очень высокой; с другой стороны, если h будет слишком низким, то это отразится на эффективности в худшую сторону. На самом деле алгоритм Дийкстры — это A* с h, установленной в ноль для всех узлов, — это, конечно, будет допустимым приближением, и этот алгоритм найдет путь, но это будет очень медленно. А еще эвристическая оценка сильно страдает от расположенных на карте порталов, мгновенно переносящих из точки в точку.

Рассмотрим способы, как добиться от A* большей эффективности в рассматриваемых областях.

Возможно, самая главная оптимизация, которую только можно сделать, — реструктуризация проблемы в более простую. Макрооператоры — это последовательности шагов, которые принадлежат друг другу и могут быть объединены в один шаг, заставляя поиск делать большие шаги за один раз. Например, самолеты делают серию шагов для того, чтобы изменить свои положение и высоту. Общая последовательность может быть использована как одно изменение состояния вместо множества маленьких отдельных шагов. Кроме того, поиск и общие методы решения задач можно значительно упростить, если разбить их на подзадачи, индивидуальное решение каждой из которых довольно простое. В случае поиска пути карту можно разделить на большие непрерывные области, чья связность известна. Выбирается одна или две граничных ячейки, которые находятся между двумя смежными областями; затем поиск производится между смежными областями, в каждой из которых путь находится для граничных ячеек.

Например, на стратегической карте Европы периода после Второй мировой войны планировщик пути, прокладывающий путь из Мадрида в Афины, может с большой вероятностью потратить кучу времени на обработку итальянского «сапога». Используя страны в качестве областей, иерархический планировщик сначала определит, что путь должен следовать из Испании во Францию, затем в Италию и из Югославии в Грецию; а путь через Италию должен вести от границы между Италией и Францией до границы между Италией и Югославией. В качестве другого примера можно привести путь из одной части здания в другую, который может быть разбит на пути между комнатами и коридорами и пути между дверьми в каждой комнате.

Гораздо проще выбирать области в предопределенных картах, чем заставлять делать это компьютер на случайно сгенерированных картах. Необходимо отметить, что обсуждаемые примеры работают в основном с обходом препятствий; для взвешенных областей желательно назначать полезные области, особенно для компьютера (они могут быть и не совсем полезные).

Непрерывное игровое пространство

Все приведенные выше методы поиска предполагали, что пространство разбито на квадратные или шестиугольные ячейки. Но что, если игровое пространство непрерывно? Что, если позиции и объектов и препятствий сохранены в виде непрерывных значений и могут быть настолько точно представлены, как и разрешение экрана? Для ответа на эти условия поиска можно заглянуть в область робототехники и увидеть какие подходы используются для мобильных роботов. Как правило, находят способы для сведения непрерывного пространства к нескольким дискретным вариантам. После этого можно использовать A* для поиска желаемого пути. Способы дискретизации пространства включают:

Ячейки; Точки видимости; Выпуклые полигоны; Квадрантные деревья; Обобщенные цилиндры; Потенциальные поля.

Замечание: существует еще немало алгоритмов поиска пути — таких как «Поиск в глубину», «Алгоритм последовательных приближений при поиске в глубину (IDDFS)», «Двунаправленный поиск в ширину» и так далее. Они представляют собой расширения и модификации рассмотренных выше основных алгоритмов.